46 Agilent E1441A Application Information
Chapter 2
Arbitrary
Waveforms
There are five built-in arbitrary waveforms stored in non-volatile memory.
You can also download up to four user-defined arbitrary waveforms into
non-volatile memory. Each waveform can contain between 8 and 16,000
data points. Topics covered on arbitrary waveforms are:
• Creating Arbitrary Waveforms
• Creating and Storing an Arbitrary Waveform
• Built-In Arbitrary Waveforms
Creating Arbitrary
Waveforms
For most applications, it is not necessary to create a waveform of any
specific length since the function generator will automatically sample the
available data to produce an output signal. In fact, it is generally best to
create arbitrary waveforms which use all available data (16,000 points long
and the full range from 0 to 4,095
DAC codes). For the Agilent E1441A, you
do not have to change the length of the waveform to change its output
frequency. All you have to do is create a waveform of any length and then
adjust the function generator's output frequency. Remember, if you create an
arbitrary waveform that includes three cycles of the same waveshape , the
output frequency will actually be three times the value you set with the
frequency command.
When creating arbitrary waveforms, you have control of both the amplitude
quantization and phase truncation errors. For example, phase truncation
harmonics will be generated when a waveform is created using the full
amplitude range of the
DAC (12 bits) but is created using only 1,000
waveform data points. In this case, the amplitude quantization errors will be
near the noise floor while the time quantization error will produce harmonics
near the -60 dBc level. Similarly, amplitude quantization harmonics will be
generated when you create a waveform using less than the full amplitude
resolution of the function generator. For example, if you use only one-fifth
of the available amplitude resolution, amplitude quantization will produce
harmonics below the -60 dBc level.
When importing data from instruments such as oscilloscopes, the data will
generally range between 1,024 and 4,096 time points and between 64 and
256 amplitude points.
When creating arbitrary waveforms, the function generator will always
attempt to replicate the finite-length time record to produce a periodic
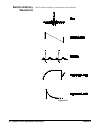
version of the data in waveform memory. As shown on the next page, it is
possible that the shape and phase of a signal may be such that a transient is
introduced at the end point. When the waveshape is repeated for all time, this
end-point transient will introduce leakage error in the frequency domain
because many spectral terms are required to describe the discontinuity.
Leakage error is caused when the waveform record does not include an
integer number of cycles of the fundamental frequency. Power from the
fundamental frequency, and its harmonics, is transferred to spectral
components of the rectangular sampling function. Instead of the expected
narrow spectral lines, leakage can cause significant spreading around the
desired spectral peaks. You can reduce leakage errors by adjusting the
window length to include an integer number of cycles or by including more
cycles within the window to reduce the residual end-point transient size.
Some signals are composed of discrete, non-harmonically related