Appendix D: Sample Waveforms
D-6 AWG710&AWG710B Arbitrary Waveform Generator User Manual
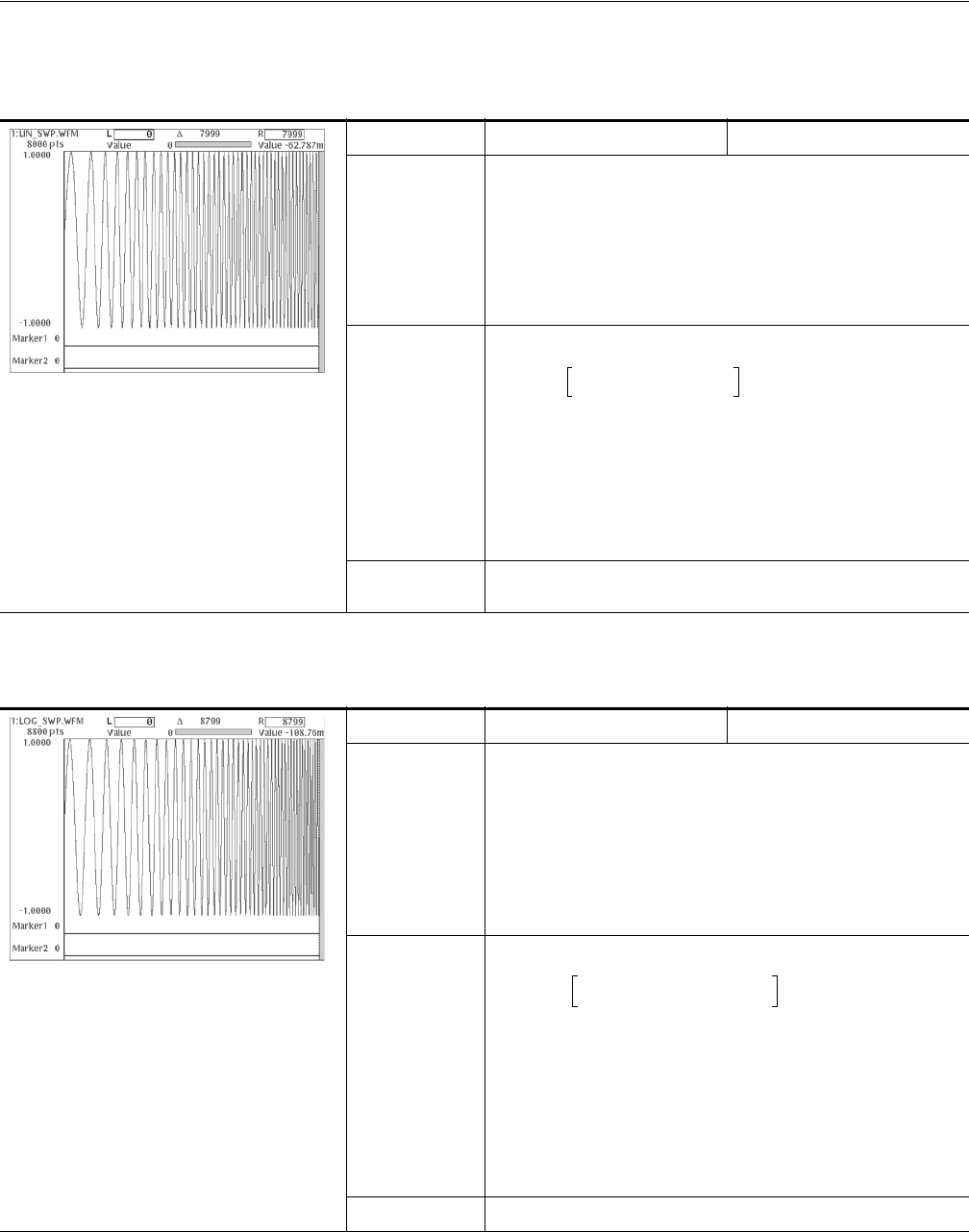
Table D-8: Linear frequency sweep
File name LIN_SWP.WFM Made with equation editor
Equation
clock = 1e9
size = 8000
k0 = 8e-6 ’sweep period
k1 = 1e6 ’start frequency
k2 = 10e6 ’end frequency
“lin_swp.wfm” = sin(2 * pi * k1 * time + 2 * pi * (k2 - k1) * (time ^ 2)/2/k0)
Descriptions
This waveform can be expressed generally by the following formula.
Here f
1
is the starting frequency, f
2
is the ending frequency, is
the initial phase, and T is the sweep period.
To assure that the phases match when this waveform is iterated, the
sweep period is set to be close to an integer multiple of the reciprocal
of the average frequency .
Settings
Waveform points: 8000, Clock frequency: 1.0 GHz, Output time:
8000 ns
Vt() 2πf
1
t 2πf
2
t
T
---
t
φ
0
+d
0
t
∫
+sin=
φ
0
f
1
f
2
+
2
--------------
Table D-9: Log frequency sweep
File name LOG_SWP.WFM Made with equation editor
Equation
clock = 800e6
size = 8800
k0 = 11e-6 ’sweep period
k1 = 1e6 ’start frequency
k2 = 10e6 ’end frequency
k3 = log (k2 / k1)
“log_swp.wfm” = sin(2 * pi * k1 * k0 / k3 * (exp (k3 * scale) -1))
Descriptions
This waveform can be expressed generally by the following formula.
Here f
1
is the starting frequency, f
2
is the ending frequency, is the
initial phase, and T is the sweep period.
To assure that the phases match when this waveform is iterated, the
sweep period is set to be close to an integer multiple of the reciprocal
of the average frequency .
Settings
Waveform points: 8800, Clock frequency: 800 MHz, Output time: 11 µs
Vt() 2 πf
1
t
T
---
In
f
2
f
1
----
⋅
exp t
φ
0
+d
0
t
∫
sin=
φ
0
f
2
f
1
–
In
f
2
f
1
----
--------------


















